BET方法，Copula模型，因子Copula模型的基本概念

a) 二项式扩展方法（Binominal Expansion Technique，BET）- 对基础资产池的假设简化，适用于同质性较强的资产池

1996年Cifuentes和O’Connor首次使用了BET的方法分析了CBO/CLO资产组合的预期损失。BET方法的基本思想是先利用分散度（Diversity Score, DS）的概念建立一个可以模仿基础资产池违约行为、包含D个同质不相关资产的虚拟资产组合，即一个为了计算期望损失分布而建立的理想组合；在分散度和原始基础资产池的违约概率确定以后，进而估计资产池的违约概率分布。由于在理想资产组合中各基础资产是同质且不相关的，因此会有D+1个违约场景：0个违约，1个违约，...，D个违约，利用二项式公式就可以求得理想资产组合的违约分布。

在使用BET方法对CLO基础资产池进行预期损失计算时，大致分为以下几个步骤：

(1)     计算CLO基础资产池的分散度:

在BET方法中，分散度被用于消除资产组合中的违约相关性。为了达到这个目的，资产池的各基础资产都被分配到适当的行业分类中。在实际运用中，以穆迪为例，分散度从两个层面上被度量：第一，从单个基础资产的层面上，将每个基础资产的面值除以平均面值以得到每个基础资产的等价单位得分，其最大值限定为1；第二，从行业类别层面上，将属于该行业的所有基础资产的等价单位得分加总得到行业总等价单位得分，然后通过一个函数将行业总等价单位得分转化为行业分散度。将所有行业的分散度加总，即可得到CLO基础资产池的分散度，用数学式可表达如下：

(2) 明确加权平均违约概率p和加权平均回收率(Weighted Average Recovery Rate，WARR):

在理想的CLO基础资产组合中，加权平均违约概率p可通过加权评级因子（Weighted Average Rating Factor,WARF）和加权平均期限（Weighted Average Life, WAL）对照理想化累计违约概率表找出。而加权平均评级因子和加权平均期限可根据各资产在资产池中的所占比例计算。

(3) 利用二项式的方法计算基础资产池中第j个资产发生违约的概率：

(4) 最后，利用式③和④，就可以算出全部D+1个违约场景的概率和对应的损失现金流，因而得到理想资产组合的预期损失：

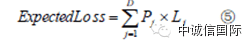
通过式⑤便可以算出CLO各分券的预期损失，从而确定各分券的信用级别。

尹占华和张文彬（2008）选取32笔经大公国际资信评估公司评级过的短期债券组成了一个基础资产池，利用了BET的方法对此资产池的预期损失分布进行了测算。两位学者认为用BET方法可以简洁方便的得到资产池的损失分布，但是用DS代替资产违约相关性只适用于同质性较强的资产池。针对此类问题，穆迪给出了以下两种改良方案。第一，当BET分析的资产池中基础资产组群异质性过强，穆迪建议使用MBET（Multi-BET）的方法。这种方法的基本思路是将原始基础资产池再划分为多个性质的子资产池，然后在运用BET方法针对每个子资产池的分布进行分析，最后将每个子资产池看作资产池的基础资产，加权计算出整个原始基础资产池的违约损失。第二，当CLO资产池中基础资产组群的集中度较高时，穆迪建议使用相关二项式方法（Correlated Binominal Method, CBM），通过增加代表性组群的相关系数来更加准确地评估由于集中度高所导致预期损失分布出现的“厚尾”现象。

b) Copula模型 - 考虑了资产违约的时间分布，充分利用Copula函数和蒙特卡罗模拟的计算方法灵活计算各分券违约损失

Copula模型的基本思想是，通过Copula函数和资产池中各基础资产的边际概率分布得到资产池的联合违约累积概率分布，配合使用蒙特卡罗模拟方法估算资产池累计预期损失，并利用损失面（Default Leg，DL）与收益面（Premium Leg，LG）预期期望值相等的关系对各分券进行信用评级。

在利用Copula模型估算资产池累计预期损失时，具体分为以下四个步骤：

（4）重复以上步骤，计算出损失面和收益面的平均值，并根据无套利原理，即可求得合理的信用价差：

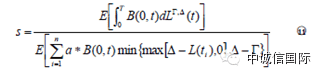
如上文描述，在运用Copula模型时，首先需要选定Copula函数。Copula函数是一种在知道边际分布和相关性结构条件下，将单变量概率分布函数连结成多元概率分布函数的有力工具。在针对CLO基础资产组合进行风险评估时，通过运用Copula函数我们就可以得到资产池中各基础资产违约时间的联合分布。Li（2000）针对如何利用Copula函数来捕捉联合违约时点进行了最早的相关研究。他经过研究发现，一个Copula函数可以将单一的边际分布函数联系成一个多元的概率分布函数。通过选定一个Copula函数种类以及相关性参数γ即可得到多个风险资产存活时间的联合概率分布函数。

Burtschell，Gregory和Laurent（2005，2009）针对不同的Copula函数进行了实证的比较分析，其中包括高斯（Gaussian）Copula函数，学生氏t（student-t） Copula函数，双t（double-t）Copula函数，Clayton-Copula函数，Gumbel Copula函数和随机相关系数Copula函数。研究结果显示，就定价目的而言，t-Copula函数和Clayton-Copula函数模型的定价结果几乎一样，并且接近高斯Copula函数模型下的定价结果；双t-Copula函数模型能更好的拟合市场报价，但是这一类模型会导致相关系数微笑；随机相关系数Copula函数得到的结果和市场上的报价误差在合理的范围内，可以很好地反应CLO的真实价值；在评价这些模型时，最重要的输入变量是违约时间的联合概率分布，它导致了用不同模型对CLO分券定价时的不同结果。

c) Copula模型 - 引入市场共同和非共同因子的概念，提高了风险评级的准确性

因子Copula模型是另一种对相关违约进行建模的方法。与上文所提及的Copula模型相比，因子Copula模型认为资产价值受市场共同因子（common factor）与非共同因子（idiosyncratic）的影响。而根据共同因子个数的不同，因子Copula模型可以被定义为单因子（one factor）和多因子（multi-factor）Copula模型。

因此，在模拟产生

的基础上，通过式13可以很快得到一次模拟的违约时间。接下来，与前文中所提到的Copula模型步骤一样，因子Copula模型也是根据无套利原理并采用蒙特卡罗模拟的方法，先模拟确定分券的损失分布、损失面和收益面，然后得到各分券的合理信用价差。

在因子Copula模型中，Y(t)和Zi(t)这两种因子的分布函数扮演了非常重要的角色。一般来说，任何分布函数都可被假定为Y(t)和Zi(t)的分布函数，但其需要经过标准化以满足分析框架中均值为0、方差为1的假设。不同的分布函数将要求不同的Copula函数对违约相关性进行建模，进而得到不同的违约损失函数。

（来源：杨路村    作者：杨珺皓）
交易技术, 交易策略

风险提示及免责条款

市场有风险，投资需谨慎。本文不构成个人投资建议，也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资，责任自负。本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！