经典证明：能否在平面上写下不可数个不相交的Y？

这篇文章收录了 Which Way Did the Bicycle Go 趣题集中一个非常有趣的问题：是否有可能在平面上画不可数个不相交的 8 ？答案是否定的。证明方法非常简单。对于任意一个 8 字形，在两个洞里各取一个有理点 P 、 Q （由于平面上的有理点是稠密的，这是总能办到的），则称这个 8 字形圈住了有理点对 (P, Q) 。注意到由于 8 字形不能相交，因此两个 8 字形不可能圈住同一对有理点。由于平面上的有理点对是可数的，因此 8 字形的数量也是可数的。

   注意到，平面上显然能够容下不可数个不相交的直线段，也显然能够容下不可数个不相交的圆（比方说一系列同心圆）。在 Mathematical Puzzles 一书里， Peter Winkler 提出了这样一个问题：我们能在平面上写下不可数个不相交的字母 Y 吗？

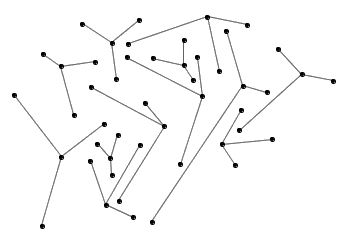
    答案是否定的。下面有一个漂亮的证明，这是由 Randy Dougherty 给出的。让我们先来看一个经典结论：假设平面上有三个红点和三个蓝点，那么我们绝不可能用线条把每一个红点和每一个蓝点都连起来，并且保证这 9 根线条互不相交（即使线条可以弯曲也不行，不信的话你可以试一试）。从图论的角度来说，就是完全二分图 K3,3 不是一个平面图。利用 Euler 公式我们可以很快证明这一点：把一个平面图的顶点数、边数和区域数（包括最外面那个无限大的区域）分别记为 V 、 E 、 F ，则 Euler 公式告诉我们 F = E – V + 2 。由于每条边都同属于两个区域，因而所有区域的平均边数为 2E / F 。在完全二分图 K3,3 中有 6 个顶点和 9 条边，若它是一个平面图，则它应该有 9 – 6 + 2 = 5 个区域，于是每个区域平均拥有 18/5 条边。这说明该图中至少存在一个边数小于 4 的区域，但对于一个二分图来说这是不可能的。

   我们把一个 Y 看作是由一个中心点、三个手臂和三个端点构成的。现在，对于平面上的每一个 Y ，我们都给它画出三个有理圆（圆心的两坐标和半径的长度都是有理数），让每个圆都圈住 Y 的其中一个端点，并且不包含 Y 的另外两臂。注意到，平面上的有理点是稠密的，半径的长度也可以任意小，因此这总是能办到的。不过，这些有理圆完全有可能和别的 Y 相交，也有可能和别的有理圆相交。我们甚至不能排除这样的情况：其中一个 Y 的某个有理圆和另一个 Y 的某个有理圆是同一个有理圆！不过，下面我们会给大家证明，三个不相交的 Y 绝不可能拥有同一组有理圆。

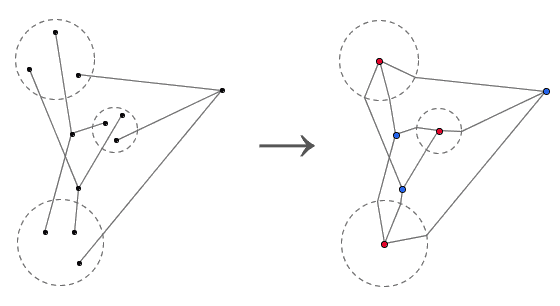
   如图，假设三个 Y 对应了同一组圆。我们修改每一个 Y 的每一条臂，让它在碰到有理圆后直接连接到这个圆的圆心。现在，把三个圆心染成红色，把三个 Y 的中心点染成蓝色，则这 9 条（修改后的）手臂就连接了所有可能的红蓝点对。然而，前面我们已经说过， K3,3 不可能是一个平面图。因此，这三个 Y 必然会相交。

   由于平面上的有理圆是可数的，因而平面上不相交的 Y 也必然是可数的。

    值得一提的是，我们这里证明的是一个相当强的结论：对于所有含有交叉点或者分岔点的图形，它在平面上都只能画出可数个（如果不允许相交的话）。这不但可以直接推出平面上不相交的 8 字形是可数的，事实上不相交的 4 或者 6 或者 9 也都只能是可数的。
金融工程, 数学算法

风险提示及免责条款

市场有风险，投资需谨慎。本文不构成个人投资建议，也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资，责任自负。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！