两个农家小孩将一块木板放在一段圆滚木上做了一个跷跷板,就一上一下地玩。请问这块木板上的每一点,在一上一下的动作中会画出怎样的一条曲线?
一个有许多木马的旋转圆盘上,一个人沿着半径以不变的速度走出走进,对地面来说他画出了怎样的一条曲线?
空地上一个等边三角形的三个顶点上有三只狗,号令一下,每只狗就去追它右边的那一只,而且方向总是向 着那一只。右边那只每转一个弯,追它的狗也照样转了弯再追。三只狗的速度全相等也都保持不变一直跑到三角形的中心才停。它们是循着怎样的曲线在追?
以上三个问题的答案乃是三种不同的螺线(spiral)。让我们先将这三种螺线稍加分析,然后再就篇幅许可看有什么有趣的问题可以介绍。
跷跷板上每一点所画的曲线称之为圆的渐伸线(invutes of circle),任何一个曲线的渐伸线都可以用以下的方法画出来。把一根线钉牢在曲线上并且拉紧,然后沿着曲线将这条线渐渐缠紧。这条线上的任何一固定点所画出来的轨迹便是曲线的渐伸线。将一只羊拴在木柱上,如果这只羊绕着柱子转,并且将拴羊的绳子紧紧缠在柱子上,这样便画出了圆的渐伸线。
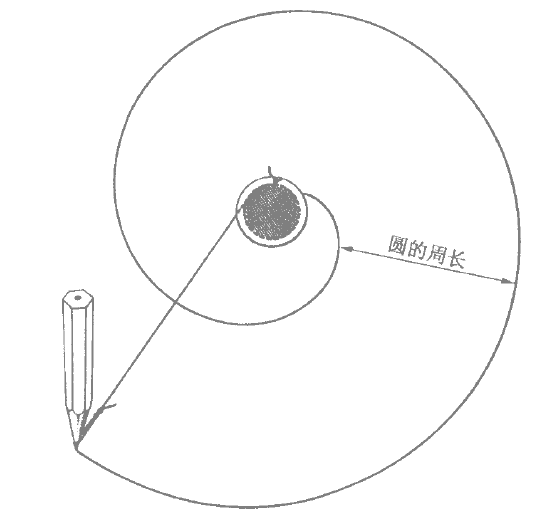
图1 画圆的渐伸线的方法
图1是画螺线的另一个简洁的方法。用一块厚纸板切出一个大小合你要求的圆片,并且粘在纸上,圆纸片上再粘一片稍稍大一点的圆片。大圆片上有个小槽以便固定一根一端打了结的绳子。把绳子在小圆片上绕上几圈绳子的另一端有一个可以让铅笔尖穿过的小孔。用铅笔将缠在小圆片上的绳子沿着小圆片松开,这就画出来一条圆的渐伸线。铅笔所画出来的螺线相邻两圈之间的距离,若沿着小圆的切线来度量则始终保持不变,和小圆周等长。圆又称之为螺线的渐屈线。
旋转木马大圆盘上的人走出的曲线称之为阿基米德螺线(spiral of Archimedes)。阿基米德最先研究这种曲线,他所写的《论螺线》(On Spirals)主要就是讨论这种曲线将一个用厚纸板切出的圆片放在唱机的转盘上,当转盘旋转时,用一支蜡笔沿着纸板上的某一半径以等速向外移动,画出来的便是阿基米德螺线。唱片上的细纹也就是最为常见的阿基米德螺线。用极坐标(par coordinate)的术语来说,任何一点的向径(radius vector)(即这一点与圆心的距离始终和它的极角(vector angle)(即它和某一固定半径之间的转角大小)保持一定的比例。在极坐标中阿基米德螺线的方程式十分简单,改用笛卡儿坐标它的方程式便复杂得多了。
另一种可以画出比较精确的阿基米德螺线的方法如图2所示。
图中的两个小圆片就是用来画圆渐伸线时所用的圆片。在这两个圆片上再钉住一条可以绕钉子旋转的长纸板条。纸板条旋转时把套在小绳一端的铅笔也同时向外移动,很容易看到,其移动的速度和纸条的旋转速度成正比,第一圈转下来之后所得到的螺线和圆的渐伸线几乎无法分辨,虽然它们是两个全不相同的曲线。阿基米德螺线每圈的距离也是相等的,但是这次的测量距离不再是沿着圆的切线方向度量,而是沿着圆的半径方向度量。阿基米德螺线和圆的渐伸线是螺线中最常见的两种。例如弹簧,卷成卷的地毯或纸卷以及一些首饰上见到的装饰花纹等等。只是这些曲线在数学上的精确度不够,不能决定它们是圆的渐伸线还是阿基米德螺线。

图2 画阿基米德螺线的工具
一旦阿基米德螺线能够精确地画出来,它便可以用来将任何一个角分成任意多个等角,包括角的三等分在内,所用的工具只限于圆规和不能度量的直尺。将这个角的顶点和螺线的极(也就是原点)重合,角的两边和螺线相交(见图3)。以P为圆心用圆规画一段圆弧AB,同时将AC三等分。分别过AC的这两个三等分点,用圆规画两段弧,和螺线相交在D、E两点。PD和PE两线就是原角的三等分线。读者不妨试试证明这种三等分角的正确性。

图3 用阿基米德螺线将任意一个角三等分
有些机器能将均匀的旋转运动改变成等速的平行运动。这些机器例如缝纫机,所用的零件就如图4所绘。图中心形两边的曲线乃是相互成镜像的阿基米德螺线。

图4 阿基米德把旋转运动变成平行运动
在等边三角形顶点上的三只狗,以等速互相追逐到中心为止。它们所画出来的曲线称之为对数螺线(logarithmic spiral),也称为等角螺线(equiangar spiral)。它的定义是:这条曲线和每一个向径的交角都是相等的。如果用数学中的点来代替狗,每一个点到达中心时所经过的路程全是相等的(都等于三角形边长的2/3)。但是在他们到达中心之前都已经绕着原点旋转了无限次!如果有两只以上的狗,每一只都由一个正多边形的顶点开始追逐,这些狗所画出来的曲线全是对数曲线。如果只有两只狗,每一只狗当然画出一条直线,反之,若有无数只狗,则它们全都沿着一个圆彼此追逐。这就粗浅地说明了等角螺线有两个极限。当它们和向径之间的角度从0变到90度时,等角螺线便从直线变成圆。
地球表面上的对数螺线称之为等斜线或菱形线(loxodrome,或 rhomb line)。这条线和地球的子午线以某一固定的角度(直角除外)相交。所以如果你在向东北方向飞行时,若一直照罗盘上某一角度行驶,你就会沿着一条等斜线一直到达北极。你所遵循的路程和追逐的狗一样,到北极有一定的距离,但是也和数学上的点一样,在你到达北极之前也绕着北极飞了无限次!你的路程在与北极相切的平而上所作之球极平面投影,乃是一条完美的对数螺线。
在自然界中,最常见的螺线就是对数螺线。例如鹦鹉螺贝壳上的条纹,蜗牛角上的条纹。许多植物种子的排列,例如向日葵和雏菊以及松果上的条纹等等,也都是对数螺线。有一种蜘蛛学名叫Epeira它所结的网的每一圈都是对数螺线。法布尔先生所写的《蜘蛛的一生》(The Life of the Spider by Jean Henri Fabre)就特别加了一篇附录,专门讨论等角螺线的数学性质及其在自然界中所见到的美丽的例子这种螺线出现在动植物上以及它与黄金分割及斐波那契数列(Fibonacci number series)之间的关系有许多文献可查。有些是十分怪异的。最重要的参考资料是库克先生所写的《生命的曲线》(The Curves of Life by Theodore Andrea Cook)。本书中的插图很多,早在1914年出版,可惜己经绝版多年。
做一个画对数螺线的工具很容易,如图5所示。也用纸板照图切出一个长条,图中a角的大小可以在0度和180度之间。将纸板的任一边固定在螺线的原点上。铅笔沿着斜边前后移动,整个纸板可以以顺时钟方向或反时钟方向紧靠着原点转动,铅笔便会画出对数螺线一段段很短的弦,而Epeira蜘蛛所织的网也是由一段段如此的短弦所成。斜边的弦越短,做出来的螺线也就越精确。这个工具也可以用来验证某一螺线是不是对数螺线。

图5 如何画对数螺线
a角如果是直角会怎样?所得到的螺线便会蜕化为一个圆假如a角等于74度39分(实际上所需的数值比此值稍大),则所得到的螺线和它自身的渐伸线是重合的。所有对数螺线的渐伸线全是对数螺线,只不过在a角等于此值时,两个对数螺线完全相同。
最早发现对数螺线的是笛卡儿(Rene Descartes)。17世纪的瑞士数学家雅各布·贝努利(Jakob Berni)对这种螺线的特性有极大的兴趣,尤其是在不同的变换下又重新出现(例如,它就是自身的渐伸线等等)。所以他留下遗言说要将对数螺线刻在他的墓碑上,并加上一句用拉丁文写的“千变万化,还我原貌”( Eadem mutata resurgo ),可惜他的遗言没有完美地完成。
首先,那句拉丁文根本给遗漏了;再者,刻墓碑的石匠因为手段不高明,刻出来的曲线又像阿基米德螺线又像圆的渐伸线。这个墓碑如今还在数学家的墓前,上面的螺线一看就知道不是对数螺线,因为圈与圈之间的距离没有越转而愈大。
若以大小而言,对数螺线最为壮观的表现就是旋转星云的星云臂。银河系本身的出现就是一个极大的神秘,而那些张牙舞爪的云臂为什么又正好是对数螺线真费人思索。这些星云臂是由大银河的旋转而产生,由一些发光的星和气体物质所组成。整个银河系是由成亿的星组成的,像一个极大的风车不停地旋转。因为我们是从旁边两个星云臂看过去的,所以地球所在的银河系看上去显得有点灰暗。根据天文学家的观察,这些银河系的中心旋转速度比外缘的旋转速度还大。根据这个观察,星云臂的旋转应该越转越紧直到没有为止才对。可是这些银河系似乎仍然无体止地转着,根本没有转到看不见为止的可能。有一种理论说那是因为这个旋转的星云臂,有一边不停地吸进发光的气体物质,另一边又不停地蒸发出去,故而始终保持原来的形状。(参见1956年9月份《科学美国人》月刊上乌尔特先生写的《银河系的进化》(The Evution of Galaxies by Jan H。 Oort)。
空间曲线中的螺旋线可以说是螺线的表兄弟,他俩的外形都是不对称的。这就是说,在一个平面上任何螺线都可以用两种不同的方法画出来,看上去完全相同,只不过彼此都是自己的镜像。如果一个螺线可以从两个相反的方向来看,例如Epeira蜘蛛网或银河系(假如我们可以跑到极远极远的太空之外的话),就可以看得出来它们不同的手向(左手或右手)。但是如果无法把一个螺线翻过来,或者无法远远地观察,那只好说有些螺线是顺时针方向,有些是反时针方向。
“顺时针或反时针方向”这种说法有时会让人更迷糊,除非说明是从曲线的中心开始重描,看它是渐渐地向外伸张或是向内收紧利用这个不易分辨的转手性,我们可以做一个游戏。首先请一位观众在一张纸的左边画一个螺线,由中心开始一步步向外伸张。画好之后就盖起来,然后移到纸的右边,并且由一个大圈开始请他再画一个向内收的螺线一般人都会不知不觉地以相反的转手性来画。画完才知道两次所画的螺线的转手性都是一样的。
在一块圆形的厚纸板上以粗的黑线画一个相当紧密的螺线,然后把它放在留声机的转盘上转。这时就会出现一个常见的幻觉,它有时看上去好像在扩大,有时又在收紧,全视原来画螺线时画的是顺时针方向或反时针方向而定。还有一个更令人惊奇的心理幻觉:你用两个不同的圆纸板画两个手向不同的螺线,再放在留声机转盘上转。先转那个扩大的螺线,同时盯着这旋转的螺线看上好几分钟然后马上转过头来看看你朋友的脸,一瞬间你朋友的脸似乎缩小了似的。换一个螺线来盯着看便会有反效果,你朋友的脸又好像在扩大似的。每一个坐火车的人都经验过类似的幻觉。坐火车朝窗外看了很久,车一停,窗外的风景好像会朝反方向移动似的。有的人用眼睛肌肉疲倦来解释,但是螺线带来的幻觉却无法如此解释。很可能是眼睛带给脑子的信号让脑子糊涂了。
Via: 《意料之外的绞刑和其他数学娱乐》【美】马丁·加德纳 著 胡乐士 译
超级数学建模 对其有节选
金融工程, 数学算法, 螺线, 数螺线
