“1”字聚会
37+37+37=111
瞧,37连加三次,和便是111。全是1。
你知道,连加后所得的和形成“1”字大聚会,还有哪些数?
将8547, 15873, 12345679分别连加,看看它们的和各是多少?
解:8547+8547+ ……+8547=111111,需要连加13个,便出现六个"1”聚会。
15873+15873+……+15873=111111,连加7个,便有六个“1"聚会。
12345679 + 12345679 + …… + 12345679 =111111111,连加九个,便有九次“1”出现在面前。
- "8”字不来
自然数的序列是1, 2, 3, 4, 5, 6, 7, 8, 9……它们像列队报到一样,整齐排列。站在后面的数都比它前面的数多1。
会算下面的算式吗?
111111111÷9=?
千万别粗心,如果商里出现了“8",那一定错了!因为“8”字藏起来了。
再算算下面的式子:

解:111111111÷9 =12345679
下面各式,都是这个算式变化的。因此,它们的结果都是12345679。只是“8”字不见了。
你觉得有趣么?
3.想要就来
1, 2, 3, 4, 5, 6, 7, 8, ……每一个数字都能引起人的丰富想象。有人说:"1字像粉笔,2字像小鸭,3字像耳朵,4字像小旗,5字像秤钩,6字像豆芽,7字像镰刀,8字像花生,9字像老爷爷的大烟袋。”
真有意思!
12345679,这几个数字中,只不见了“8"。而“8”字多么像香喷喷的花生,你想见到它吗?
可以!只要用8的9倍数去乘12345679,便可出现一长串8:
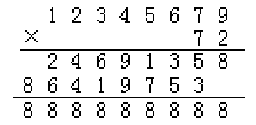
哇,全是8!
其实,只要你用一个合适的数去乘12345679,任何一个你喜欢的数字“想要就来”。
你知道这些乘数吗?
解:因为12345679 X 9 =111111111
所以,想要几,就用9的几倍作乘便可以了。如,想要5,便用45 ( = 9X5)作乘数即可。
4.成群结队
看看下面的算式,又一种奇妙的现象出现了!
12345679 × 12=148148148
12345679 × 15=185185185
12345679 × 21=259259259
12345679 × 24=296296296
12345679 × 27=333333333
12345679 × 30=370370370
12345679 × 33=407407407
12345679 × 36=444444444
12345679 × 39=481481481
瞧,结果总是三个数字重复出现,真像结伴而行的几个好朋友。它们总是互相联手,不肯分离。
你知道,要想得到这样的结果,有什么规律?
解:被乘数12345679没有变化,乘数分别是12、15、 18、21、24……
后一个乘数依次比前一个乘数都多3,得出的结果才能是三个数字循环出见,纷至沓来。
首到12345679 × 78=962962962仍然符合“成群结队”规律,可是,令人奇怪的是:当乘数超过“78”时,这种奇妙的现象便销声匿迹,不再出现了。
5.只问8数
观察下列各式:
1 × 9=9
11 × 99=1089
111 × 999=110889
1111 × 9999=11108889
……
请问:这样的被乘数和乘数各是十位数,积中应含有多少个8?
解:观察已知的算式:一位数相乘时,积没有8。两位数相乘时,积含有一个8。三位数相乘时,积含有两个8。四位数相乘时,积含有三个8……
这表明积含有8的个数总比因数的位数少1。所以,因数若是十位数,积含有8的个数是10-1=9个。
金融工程, 数学算法
