本罗特·曼德尔布洛特倚靠着一幅著名的分形背景图。这幅分形图是他创造的,具有可以无限展开的结构。
一个简单而充满疑惑的问题开启了一种新的几何学不同寻常的故事。英国的海岸线究竟有多长?我们可以拿出一份地图,参照它的标尺,用一把尺子来对英国海岸线的长度做出粗略的估计。但如果我们用一把刻度更小一点的尺子,重新进行测量,将得到一个更长的海岸线。如果我们驾驶飞机沿着海岸,从空中截取图片来进行测量,我们将看到海滩和海岸曲曲折折,有的向内凹陷,有的向外突出,最终测得的结果将会更长。最后,我们还可以以我们自己的步子为尺度从海滩出发,开始测量。
看来,无论是英国还是加利福尼亚的海岸,都具有一种特殊的属性,如果不断地放大,就能不断地增加细节的水平,永远没有尽头。海岸线的长度看起来几乎是无限的,至少可以不断地放大,直到原子水平。
数学家把对这种可以无限细节化的客体描述叫做分形几何学。在探索这种层次无限但又具有自相似结构的固定模式的新几何学时,本罗特·曼德尔布洛特(Benoit Mandelbrot)在看起来似乎混沌的自然现象背后,发现了潜隐的秩序。
不可思议的聚合
1958年,曼德尔布洛特接受了IBM公司开放实验室的研究职位,他的有关研究兴趣最终开始走向整合。IBM公司开始成为计算机行业的领导者,并且和贝尔电话公司一样,它有一种宽松的政策,就是拿出一些钱来设立实验室,并供给那些科学新锐们相对自由地从事他们感兴趣的研究。尽管他们资助的研究工作可能于计算机或没有直接或即时的联系,但是这些研究成果最终可能导致技术的巨大进步。
1961年,IBM公司委托曼德尔布洛特分析电话线路中经常出现神秘噪音的间题。IBM公司认为这些噪音产生的原因可能是工人们维修系统的工具。然而,曼德尔布洛特注意到,这些噪音有一种类似于布朗运动的特殊结构。他仔细分析噪音时发现,一个大的噪音爆发背后往往是若干更小的噪音爆发的集簇。这些噪音是这种线路结构自身固有结构的产物。基于曼德尔布洛特的工作,IBM取消了一项昂贵而无效的反噪音项目。
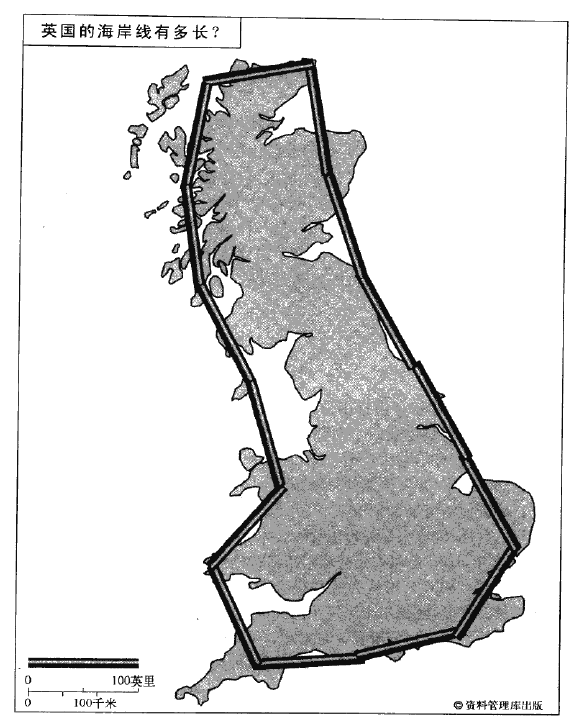
曼德尔布洛特在他著名的分形论文中一开始就问,“英国的海岸线有多长?”用长度固定的小棒沿着地图上海岸线边缘摆放,能够浏到一个海岸线的大致长度。然而,海岸线的任何一个区域都可以被“吹胀摊开”并重新测量。受德尔布洛特声称海岸线是一个分形的结构,其长度事实上是无限的。
与此同时,曼德尔布洛特开始将目光从研究“噪音”这类随机值转向其他类型的数据。尽管他对经济学领域没有任何背景,但他认为这一领域有着大量的随机数据资源,因为通常能够查到数百年价格变化的详细记录。大多数经济学家认为商品价格的变化(比如棉花)通常受两方面因素的驱动。一方面是一些可以解释的因素,比如坏天气导致棉花产量下降,结果造成价格上涨。另一方面的原因则是不确定的或者说是随机的价格波动,可能每天甚至每小时价格都会有微小的变动。
经济学家们认为如果将随机价格波动绘制在一张图中,那么将会呈现一种著名的钟形曲线的模式。当我们用字母A-F来给曲线分段标定等级,就会发现处在两端A等和F等的个体很少,而处在B等和D等的相对多一些,处在C等的最多。钟形曲线在C等中央凸起,向A等和F等两个方向依次变小,直至消失。也就是说,曼德尔布洛特期望大多数价格都在平均价值附近盘旋。
曼德尔布洛特应哈佛大学经济学教授亨雷克·豪塔克(HendrickHouthakker)之邀请,访间哈佛大学并给学生做演讲。当曼德尔布洛特走进豪塔克办公室的时候,看到黑板上的一幅图竟然似曾相识。’原来,曼德尔布洛特曾经画过一幅人群收人的分布图,他发现收人图并不是一个完美的钟形曲线,它们趋向于在尾端有一个更长的、更夸张的聚合。豪塔克的图看起来和曼德尔布洛特的图极为相似,尽管他的图表达的是棉花价格而不是人群收人的分布。
混沌与分形
这种奇异的现象不仅出现在收人与棉花价格的波动上,也出现在物理学中的布朗运动和湍流以及大气运动模式,还出现在曼德尔布洛特早期关于电话噪音的研究中。在几何学中,这体现为一种表面看起来是随机分布构成的细小集簇而构成的模式。这种模式并不像欧氏几何那样具有整齐的直线和平滑的曲线。这种模式具有自相似的结构,也就是说,如果把这个模式放大,其中每个部分看起来都是整体的一个缩影。使用更小的尺度,可以无限制地做下去。曼德尔布洛特用“分形”〔fractal,意思是破碎的或者被打碎了的)这个词来描述这些几何模式。
曼德尔布洛特集

这个曼德尔布洛特集是用Fractint for Windows产生的。许多软件包(大部分是免费的)都能够产生分形图案。
20世纪60年代,计算机开始从真空电子管向晶体管转变。当时计算机还是一种十分昂贵的商品,曼德尔布洛特和他的助手们不得不花上数周的时间来计算分形模式,而这些计算在现代的家用电脑上仅仅需要几秒钟时间。
曼德尔布洛特的研究中最复杂最美丽的发现是后来被称作曼德尔布洛特集的著名图案。若干年以前,曼德尔布洛特曾手工绘制了它的草图,主要是基于20世纪初期两位法国数学家的工作,他们是加斯顿·朱丽叶(Gaston Jia)和皮埃尔·费都(Pierre Fatou) 。曼德尔布洛特在大学时代曾阅读过他们的论文,当时仅仅是一些对于数学朦胧的好奇心。
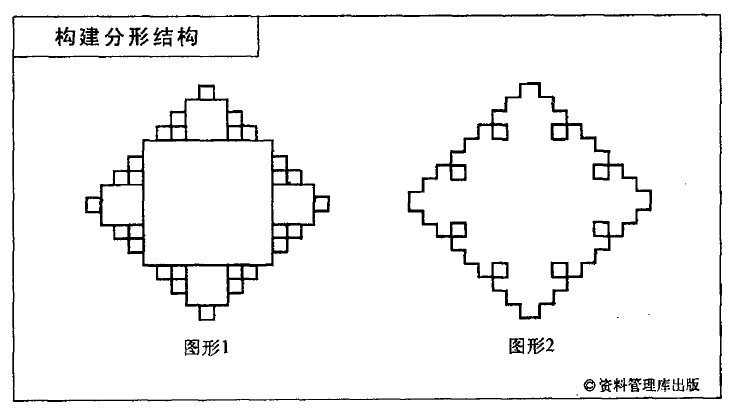
上例中呈现的是构建分形结构的简单方法,可以不断的重复绘制矩形,每个矩形的边长都是前一层次矩形边长的三倍。图2是将图1中的内部矩形擦去,以便更清晰地呈现分形结构。
现在计算机已经让一系列朱丽叶集的实际实现成为可能。曼德尔布洛特程序在一个类似于高中几何中学过的笛卡尔坐标系的栅格中绘制图形,所不同的是它包含着复数—这一他们想象的成分。他设计程序的原始版,只能绘制出一些对称的圆盘状图形。后来,程序的改进版大大增加了运算量,但曼德尔布洛特好像发现了细微图点的模糊集簇。起初,他以为是计算机的数字程序出了间题,随后他把程序放在更大的ABM机器上运行,结果发现这些模糊的点,竟然可以分解为一系列错综复杂的螺旋形的卷须状图形,就像用一个更好的望远镜观察银河系的星云一样。
曼德尔布洛特集多刺的螺旋形图案和生气勃勃的细丝(可以在图形显示器上看到)展现了一种永无止境的奇异结构,这种结构在任何水平的细节层次上都具有一致性。然而这整个复杂的图形都是由一个并不十分复杂的方程经过简单的反复叠代而形成的。当时还处在计算机的童年时代,随着更强大的计算机的不断升级,从一个简单的规则出发创造出一个永无止境的复杂模式,已经成为可能的事情了。
20世纪80年代,曼德尔布洛特成为一位公众演讲家。自从1967年在一篇论文中介绍过海岸线分形以来,他常常用英国海岸线来作为快速理解分形几何的一个经典例证。海岸线虽然被无限放大但褶皱依然存在着,是一个十分形象化的例子,便于公众理解。海岸线是分形的,和仅仅拥有一维的线(地图上的一条线)不一样,它拥有一个分形维度,大约是1.2。
换一种说法就是,海岸线在它的单维空间中有许许多多格外突出的锯齿和曲折。应用价值的发现尽管我们已经能够在媒体中看到各种五彩缤纷的分形图案,但是许多科学家们对曼德尔布洛特集的应用价值的认识十分迟缓,甚至很难接受。因为毕竟既存的统计方法已经能够近乎完美地处理大多数的应用问题,并且传统统计结果的图表工整又便于理解。分形和混沌理论涉及一些怪异的形状和不可预测的分布,乃是一种新的数学。那些接受传统几何学训练的数学家们有时缺乏曼德尔布洛特式的直觉能力,难以理解虽然怪异但却熟悉而相似的形状。
20世纪70年代,曼德尔布洛特和其他研究者将分形几何学和混沌行为理论应用到自然的许多方面。例如,在生物学领域,分形可以应用于分析藏类植物的结构,分析细菌的繁殖与生长,甚至于分析人体循环系统的分支情况。天文学方面,发现土星环具有分形结构,发现银河系的星体聚合具有分形结构。
基于分形学,也发展出了许多实用技术。比如,可以运用分形辨别图片是自然图片还是人工图形,因为自然图片具有分形结构。分形技术可以用近似方程代替重复的结构,还被应用于数字图像的压缩。
相关链接:制造分形与应用分形
20世纪60年代起,各种不同类型的分形图形开始被发现。每个分形图形都可以由一个方程产生,这些方程包含一系列复数—这些数不仅包括“正常值”(即实数,比如整数、分数等),还包括一些“想象数”(即数学上的虚数),比如-1的平方根等。创造和应用虚数主要是为了让数学系统更加一致和完备,而且它们也的的确确和许多自然现象具有一致性。
曼德尔布洛特第一次创作分形图案时,他使用的是IBM大型计算机,当时还要依靠打孔卡片来进行信息输入。如今,任何一台桌面个人计算机都能更简易地运用所有颜色创作分形图案,并将之呈现在屏幕上。
现在有大量免费或廉价的软件程序,可以让我们在计算机上独自创作分形图案。更复杂的程序(包括Adobe Photoshop的滤镜)能够依据各种图像和纹理创作分形图形。由于分形具有深层和连续变化的结构,所以也常常用于产生各类数字地形图,被广泛运用在科幻电影和视频游戏等数字艺术中。
其他科学家:克里斯朵夫·斯库兹
地球学家克里斯朵夫·斯库兹(Christopher Schz)开始研究从20世纪60年代以来的地震分布。斯库兹和地震学家了解到有时候地震爆发的频率拄拄有一种以不同规模聚合的倾向。没有人知道这种聚合模式的意义,也没有人明白这种聚合的成因。斯库兹决定进一步深入研究。
当斯库兹在麻省理工学院时,很少听说曼德厂尔布洛特及其他的工作,但是在1978年,斯库兹看到了一本书,这本书包含着各种美妙的图案和生僻的方程。这本书就是曼德尔布洛特的《分形对象:形,机遇和维度》。面对曼德尔布洛特提出的一系列惊·异的观念和思索,斯库兹一开始并不敢确定就一定能够应用来解决地震问题。但是他开始用分形的眼光来分析地球,他仔细地考察了地表和地下的全部裂缝与凸起,包括地震的给果,以及各种液体流动和压力的造就的分形杰作。分形几何学是描述这些结构和交互作用的理想工具。在詹姆斯·格雷克(James Gleick)的《混沌:开创一种新的科学》一书中,斯库兹指出:
这是一个能够让我们对付地球一这个维度不断变化的物体的模型。它给予你数学和几何工作,你可以用之来进行描述和预测。一旦你越过了这座小山·峰,一理解了这个范式,你就能用一种新的方式来测量和思考事物。你将会用完全不同的眼光看待它们,从而拥有新的创见。一这种视南与传统完全不同,它更开阔。
Via:《数学:描绘自然与社会的有力模式》 (美)哈里·亨德森著 王正科 赵华 译
原文有节选
金融工程, 数学算法
