转自:超级数学建模(微信ID: supermodeling)
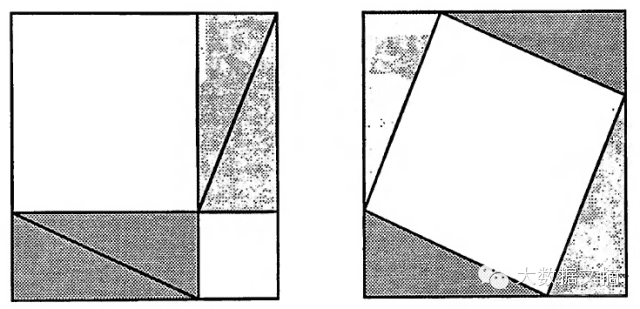
勾股定理Ⅰ
改编自Chow pei suan.ching(作者不明,大约公元200年)
adapted from the Chou pei suan..ching (author unknown, circa B.C. 200?)
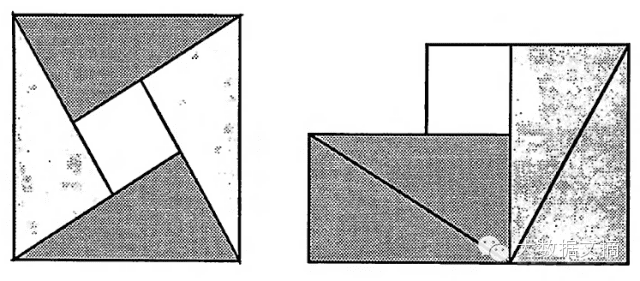
勾股定理Ⅱ
Bhaskara(12th century)
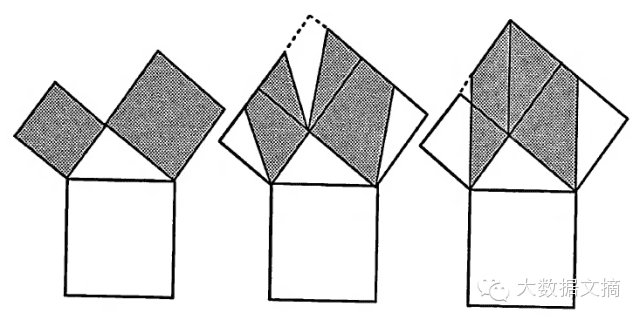
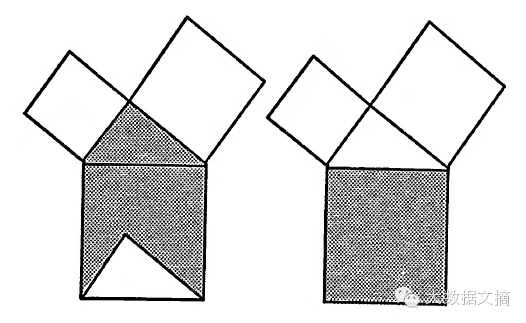
勾股定理Ⅲ
基于欧几里得的证明(based on Euclid' proof)
勾股定理Ⅳ
H.E. Dudeney(1917)
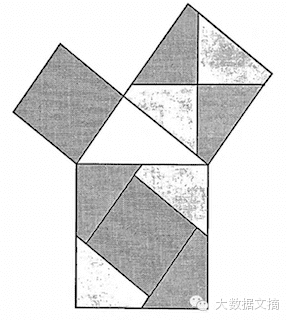
勾股定理Ⅴ
詹姆斯·艾伯拉姆·加菲尔德(1876)【美国第20任总统】(James A. Garfield)
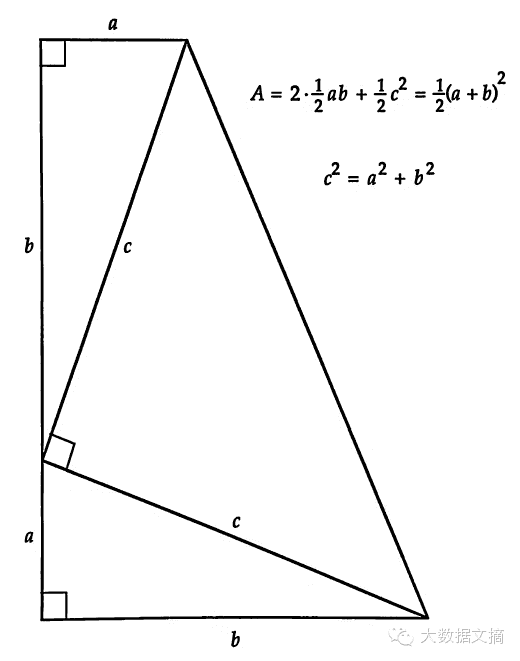
勾股定理ⅥMichael Hardy
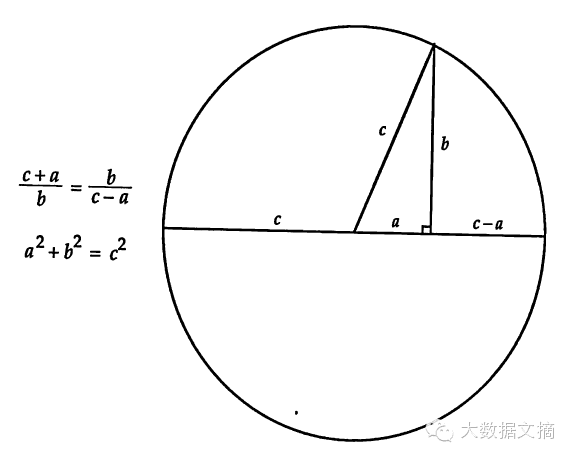
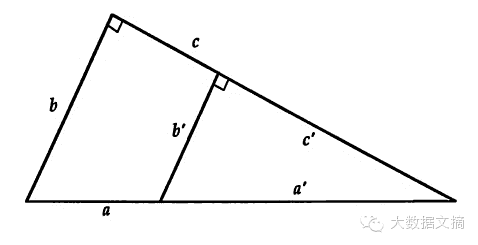
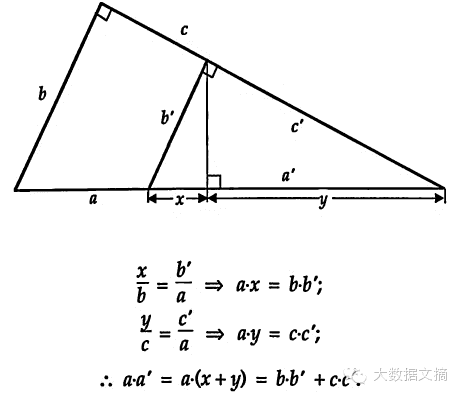
勾股定理:a·a'=b·b'+c·c'A Pythagorean Theorem: a·a'=b·b'+c·c'
Enzo R. Gentile
来源:
Proofs Without Words: Exercises in Visual Thinking
Authored by Roger B. Nelsen
超级数学建模对其有节选
数据分析, 数据挖掘
