

数学突破奖:告诉你一个真实的数学研究
科学是目前人类探知客观世界最好的方式。尽管投入科学不能一蹴而就地得到切实有用的成果,但长远来看却是技术发展最好的动力源。与技术开发不同,对科学的投入更像是公益活动,因为科学研究得到的成果属于全人类。而数学作为科学的“语言”,也有着类似的性质
数学中竟然还有这样的定理!
谁说数学是枯燥的?在数学里,有很多欢乐而又深刻的数学定理。这些充满生活气息的数学定理,不但深受数学家们的喜爱,在数学迷的圈子里也广为流传。喝醉的小鸟定理:喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家。假设有一条水平直线,从某个
八卦之王:社交网络中谁最八卦?
随着对社交网络(social network)研究的不断深入,一个现实的问题一直困扰着政策制定者和社交网络中的个人:可不可以识别出哪些人在一个社交网络中对信息传播有最强的影响力?或者说,社交网络中的个人究竟会不会知道社交网络中谁是影响力最大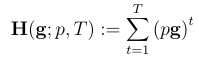
让你立刻爱上数学的10个算术游戏
我们经常被问到:数学到底哪里有趣了,数学之美又在哪里?这篇文章精心选择了 10 个老少咸宜的算术问题,以定理、趣题甚至未解之谜等各种形式带领大家窥探数学世界的一角。不少问题背后都蕴含了深刻的数学知识,触及到数学的各个领域。希望从小数学就不及
数学之美系列六:图论和网络爬虫?(Web Crawlers)
离散数学是当代数学的一个重要分支,也是计算机科学的数学基础。它包括数理逻辑、集合论、图论和近世代数四个分支。数理逻辑基于布尔运算,我们已经介绍过了。这里我们介绍图论和互联网自动下载工具网络爬虫 (Web Crawlers) 之间的关系。顺便
数学里也能耍流氓
数学一向以严谨的思维著称,每一步推理都需要严格的理由。但在数学历史中,漏洞百出的数学推理也频频出现。有趣的是,即使是这些不严格的思路也充满着智慧,在数学中的地位不亚于那些伟大的证明。今天,果壳死理性派会用几个经典例子告诉你,在数学里也是可以
数学之美系列四:怎样度量信息?
前言: Google 一直以 “整合全球信息,让人人能获取,使人人能受益” 为使命。那么究竟每一条信息应该怎样度量呢?信息是个很抽象的概念。我们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信
4.3亿人次狂欢?大数据告诉你锋菲恋到底有多火
阿里的公关团队使出吃奶的劲头,找到了8个普通人来纽约敲钟——多好的故事——想不上头条都难的故事。谁知道几小时过后,搜狐娱乐早上7点40分推出王菲谢霆锋“世纪大复合”的消息。周末睡醒起来,什么王全安嫖娼张雨琦表示“共同面对”,什么姚晨“物是人
数学之美系列三:隐含马尔可夫模型在语言处理中的应用
前言:隐含马尔可夫模型是一个数学模型,到目前为之,它一直被认为是实现快速精确的语音识别系统的最成功的方法。复杂的语音识别问题通过隐含马尔可夫模型能非常简单地被表述、解决,让我不由由衷地感叹数学模型之妙。自然语言是人类交流信息的工具。很多自然
谷歌背后的数学
在如今这个互联网时代, 有一家家喻户晓的公司, 它自 1998 年问世以来, 在极短的时间内就声誉鹊起, 不仅超越了所有竞争对手, 而且彻底改观了整个互联网的生态。 这家公司就是当今互联网上的第一搜索引擎: 谷歌 (Google)。在这样一
数学建模如何诱骗了华尔街
现实世界——从种族隔离制度到金融市场——一直在警示我们:那些试图通过科技来掌握复杂人类行为的做法会使我们误入歧途。无论是在科学领域,还是在日常生活中,我们都经常会做出一些幼稚的事:我们坚持把未知的事物放进我们构想出来的模型里,坚持事实和我们
